Rotting Oranges
Table of Contents
Problem Statement
Rotting Oranges
You are given an m x n grid where each cell can have one of three values:
0representing an empty cell,1representing a fresh orange, or2representing a rotten orange.
Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.
Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.
Example 1
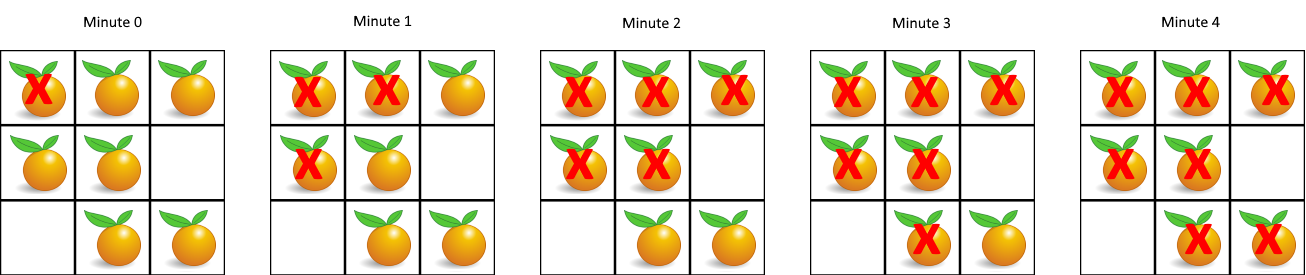
Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4
Example 2
Input: grid = [[2,1,1],[0,1,1],[1,0,1]] Output: -1 Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.
Example 3
Input: grid = [[0,2]] Output: 0 Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 10grid[i][j]is0,1, or2.
Golang Solution
//practice rotting oranges
package main
import "fmt"
func orangesRotting(grid [][]int) int {
// logic
// we need to use bfs
// 1. Starting vertex needs to be x,y where value is 2
// 2. Traverse over matrix once, to get list of all vertex with value as 2
// 2.1 Add all this vertex in queue
// 3. In same iteration, also count total number of fresh oranges
// 3.1 if totalFreshOranges are 0, then we can return 0
//minElapsed := 0
//While queue is not empty
// 4. Increase minElapsed : minElapsed++
// Get current queue size and iterate over to that size only
// 4.1 If value is 2, then visit all neighbours,
// 4.2. i.e. add next values in current row, col to get newRow, newCol {1,0} , {0,1}, {-1,0}, {0,-1}
// check boundaries on newRow and newCol are within matrix maxRow, maxCol
// 4.3 mark fresh oranges as rotten as part of visiting neighbours
// 4.4. Add new neighbour in queue
maxRow := len(grid)
maxCol := len(grid[0])
queue := [][2]int{}
totalFreshOranges := 0
for row, entries := range grid {
for col, value := range entries {
if value == 2 {
queue = append(queue, [2]int{row, col})
} else if value == 1 {
totalFreshOranges++
}
}
}
if totalFreshOranges == 0 {
return 0
}
minElapsed := 0
nc := [][]int{{1, 0}, {0, 1}, {-1, 0}, {0, -1}}
for len(queue) > 0 && totalFreshOranges > 0 {
// 4.1 If value is 2, then visit all neighbours,
// 4.2. i.e. add next values in current row, col to get newRow, newCol {1,0} , {0,1}, {-1,0}, {0,-1}
// check boundaries on newRow and newCol are within matrix maxRow, maxCol
// 4.3 mark fresh oranges as rotten as part of visiting neighbours
// 4.4. Add new neighbour in queue
currentSize := len(queue)
for i := 0; i < currentSize; i++ {
current := queue[0]
queue = queue[1:]
for _, v := range nc {
newRow := current[0] + v[0]
newCol := current[1] + v[1]
if newRow >= 0 && newRow < maxRow && newCol >= 0 && newCol < maxCol && grid[newRow][newCol] == 1 {
totalFreshOranges = totalFreshOranges - 1
grid[newRow][newCol] = 2
queue = append(queue, [2]int{newRow, newCol})
}
}
}
minElapsed++
}
if totalFreshOranges != 0 {
return -1
}
return minElapsed
}
func main() {
grid := [][]int{
{2, 1, 1},
{1, 1, 0},
{0, 1, 1},
}
//grid := [][]int{
/// {2,1,1},
// {0,1,1},
//{1,0,1},
//}
//grid := [][]int{
// {0, 2},
//}
fmt.Printf("rotten oranges=%d\n", orangesRotting(grid))
}
Clean version
package main
import "fmt"
func orangesRotting(grid [][]int) int {
maxRow := len(grid)
maxCol := len(grid[0])
queue := [][2]int{}
totalFreshOranges := 0
// Step 1: Initialize the queue with all rotten oranges and count fresh ones
for row, entries := range grid {
for col, value := range entries {
if value == 2 {
queue = append(queue, [2]int{row, col})
} else if value == 1 {
totalFreshOranges++
}
}
}
// If there are no fresh oranges, return 0 as there's nothing to rot.
if totalFreshOranges == 0 {
return 0
}
minElapsed := 0
neighbors := [][]int{{1, 0}, {0, 1}, {-1, 0}, {0, -1}}
// BFS traversal
for len(queue) > 0 && totalFreshOranges > 0 {
currentSize := len(queue)
for i := 0; i < currentSize; i++ {
current := queue[0]
queue = queue[1:]
// Check all four possible neighbors
for _, direction := range neighbors {
newRow := current[0] + direction[0]
newCol := current[1] + direction[1]
// If within bounds and there is a fresh orange, make it rotten
if newRow >= 0 && newRow < maxRow && newCol >= 0 && newCol < maxCol && grid[newRow][newCol] == 1 {
grid[newRow][newCol] = 2
totalFreshOranges--
queue = append(queue, [2]int{newRow, newCol})
}
}
}
minElapsed++
}
if totalFreshOranges > 0 {
return -1
}
return minElapsed
}
func main() {
grid := [][]int{
{2, 1, 1},
{1, 1, 0},
{0, 1, 1},
}
//grid := [][]int{
// {2,1,1},
// {0,1,1},
// {1,0,1},
//}
//grid := [][]int{
// {0, 2},
//}
fmt.Printf("rotten oranges=%d\n", orangesRotting(grid))
}
Output
rotten oranges=4
Program exited.Solution Outline
1. Identify Key Requirements
- Track the time taken for all reachable oranges to rot.
- Simulate the spread of rot minute by minute.
- Stop if no more oranges can rot or if all reachable oranges have rotted.
2. Use BFS for Efficient Traversal
- BFS (Breadth-First Search) is ideal because it processes nodes (oranges) in layers, which naturally aligns with tracking the “minutes” in the spread of rot.
- Each level of BFS represents one minute of spreading rot.
3. Initialize the BFS Queue
- Add all initial rotten oranges to the queue. This queue will hold the position of each rotten orange as it spreads.
- Count the fresh oranges to track if they all rot by the end of the process.
4. Define Directions for Neighboring Cells
- Use an array of coordinate pairs to represent possible adjacent cells: up, down, left, and right.
5. BFS Execution Loop (Minute-by-Minute Rot Spread)
- Process all oranges in the queue at the current level (minute).
- For each rotten orange, spread the rot to adjacent fresh oranges.
- Update the grid to mark newly rotten oranges and add them to the queue.
- Increment the timer (minute counter) after each level of BFS.
6. Check Completion Conditions
- After the BFS completes, check if any fresh oranges remain.
- If all fresh oranges rotted, return the time taken (in minutes). If any fresh oranges remain unrotted, return
-1.
Code Implementation (Pseudocode)
- Initialize Queue and Count Fresh Oranges
- Initialize a queue with all initially rotten oranges.
- Count all fresh oranges to check if we’ve rotted all by the end.
- Define Directions for Adjacent Cells
- Set directions as: up, down, left, right.
- Process Each Level of BFS (Each Minute)
- While the queue isn’t empty:
- Increment the timer.
- For each rotten orange in the queue:
- Spread rot to all adjacent fresh oranges.
- If any fresh oranges rot, add them to the queue and decrement the fresh count.
- While the queue isn’t empty:
- Check for Remaining Fresh Oranges
- If fresh count is
0, return the timer. - If fresh oranges remain, return
-1(indicating some oranges are unreachable).
- If fresh count is
Complexity Analysis
- Time Complexity: O(n * m) where
nis the number of rows andmis the number of columns. Each cell is processed once. - Space Complexity: O(n * m) for the queue storing coordinates of rotten oranges.
Edge Cases
- No Fresh Oranges: Return
0immediately as all oranges are already rotten. - No Rotten Oranges Initially: If there are fresh oranges and no rotten ones, return
-1. - Isolated Fresh Oranges: If fresh oranges are isolated by empty cells, they will remain unrotted, so return
-1.
Conclusion
The BFS approach is optimal for the Rotting Oranges problem as it naturally aligns with the spread of rot layer by layer, each layer representing one minute.
By processing the grid level by level, we effectively calculate the minimum time required for all reachable fresh oranges to rot, or we determine if some fresh oranges cannot rot due to isolation.
Visit https: https://codeandalgo.com for more such contents