Minimum Number of Arrows to Burst Balloons
Table of Contents
Minimum Number of Arrows to Burst Balloons
Problem Statement
There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array points where points[i] = [xstart, xend] denotes a balloon whose horizontal diameter stretches between xstart and xend. You do not know the exact y-coordinates of the balloons.
Arrows can be shot up directly vertically (in the positive y-direction) from different points along the x-axis. A balloon with xstart and xend is burst by an arrow shot at x if xstart <= x <= xend. There is no limit to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.
Given the array points, return the minimum number of arrows that must be shot to burst all balloons.
Example 1:
Input: points = [[10,16],[2,8],[1,6],[7,12]] Output: 2 Explanation: The balloons can be burst by 2 arrows: - Shoot an arrow at x = 6, bursting the balloons [2,8] and [1,6]. - Shoot an arrow at x = 11, bursting the balloons [10,16] and [7,12].
Example 2:
Input: points = [[1,2],[3,4],[5,6],[7,8]] Output: 4 Explanation: One arrow needs to be shot for each balloon for a total of 4 arrows.
Example 3:
Input: points = [[1,2],[2,3],[3,4],[4,5]] Output: 2 Explanation: The balloons can be burst by 2 arrows: - Shoot an arrow at x = 2, bursting the balloons [1,2] and [2,3]. - Shoot an arrow at x = 4, bursting the balloons [3,4] and [4,5].
Constraints:
1 <= points.length <= 105points[i].length == 2-231 <= xstart < xend <= 231 - 1
Logic
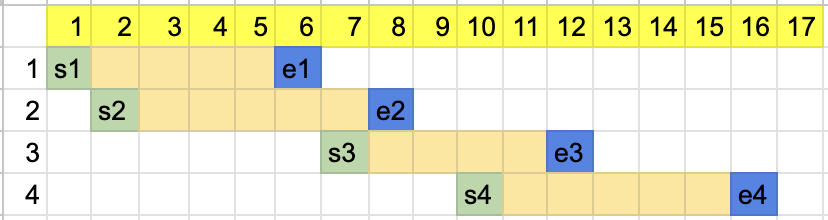
- Definition of Overlap:
Two intervals[start1, end1]and[start2, end2]overlap ifstart2 <= end1. This means the second interval starts before or exactly when the first interval ends. - Updating the Overlap:
When two intervals overlap, merge them into a single interval by taking:start = start2(start of the current interval).end = min(end1, end2)(the smaller of the two endpoints to maintain the tightest overlap).
- Arrow Count Reduction:
If there’s an overlap, a single arrow can handle both intervals, so reduce the total arrow count by 1. - Non-Overlapping Intervals:
If the intervals do not overlap (start2 > end1), a new arrow is needed for the current interval, and the overlap logic resets with the current interval as the new reference.
Golang Solution
//452. Minimum Number of Arrows to Burst Balloons
func findMinArrowShots(points [][]int) int {
sort.Slice(points, func(i, j int) bool {
return points[i][0] < points[j][0]
})
n := len(points)
// we are setting number of arrows required for each intervals to number of intervals
// This is worst case if none of the intervals are overlapping
result := n
previous := points[0]
for i := 1; i < n; i++ {
current := points[i]
// check if intervals are overlapping
if current[0] <= previous[1] {
// update merge points by taking
// common portion from both intervals
previous = []int{
current[0], // start
min(current[1], previous[1]), // end
}
// if the intervals are overlapping,
// then we can reduce the arrow required by 1
result = result - 1
} else {
// if interval is NOT overlapping
// then move the previous point to current
previous = current
}
}
return result
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
Output
Input
points = [[10,16],[2,8],[1,6],[7,12]]
Output
2Please visit https: https://codeandalgo.com for more such contents