Lowest Common Ancestor of a Binary Tree
Table of Contents
Problem Statement
Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Example 1:
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 Output: 3 Explanation: The LCA of nodes 5 and 1 is 3.
Example 2:
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 Output: 5 Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
Example 3:
Input: root = [1,2], p = 1, q = 2 Output: 1
Constraints:
- The number of nodes in the tree is in the range
[2, 105]. -109 <= Node.val <= 109- All
Node.valare unique. p != qpandqwill exist in the tree.
Golang Solution
// lowest common ancestor
package main
import (
"fmt"
)
type TreeNode struct {
Left *TreeNode
Right *TreeNode
Val int
}
func addNode(root *TreeNode, val int) *TreeNode {
if root == nil {
return &TreeNode{
Val: val,
}
}
if root.Val > val {
root.Left = addNode(root.Left, val)
} else {
root.Right = addNode(root.Right, val)
}
return root
}
func createTree(values []int) *TreeNode {
var root *TreeNode
for _, val := range values {
root = addNode(root, val)
}
return root
}
func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
if root == nil || root == p || root == q {
return root
}
left := lowestCommonAncestor(root.Left, p, q)
right := lowestCommonAncestor(root.Right, p, q)
if left != nil && right != nil {
return root
}
if left == nil {
return right
}
return left
}
func findNode(root *TreeNode, val int) *TreeNode {
if root == nil || root.Val == val {
return root
}
left := findNode(root.Left, val)
if left != nil {
return left
}
return findNode(root.Right, val)
}
func findLCA(root *TreeNode, n1, n2 int) *TreeNode {
m1 := findNode(root, n1)
m2 := findNode(root, n2)
return lowestCommonAncestor(root, m1, m2)
}
func preOrderTraversal(root *TreeNode, result *[]int) {
if root == nil {
return
}
*result = append(*result, root.Val)
preOrderTraversal(root.Left, result)
preOrderTraversal(root.Right, result)
}
func postOrderTraversal(root *TreeNode, result *[]int) {
if root == nil {
return
}
postOrderTraversal(root.Left, result)
postOrderTraversal(root.Right, result)
*result = append(*result, root.Val)
}
func inOrderTraversal(root *TreeNode, result *[]int) {
if root == nil {
return
}
inOrderTraversal(root.Left, result)
*result = append(*result, root.Val)
inOrderTraversal(root.Right, result)
}
func main() {
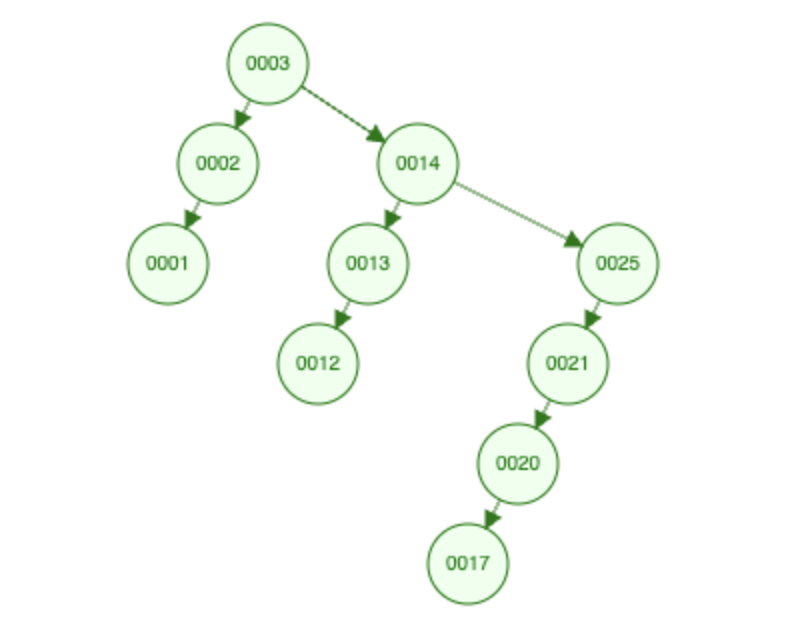
values := []int{3, 14, 13, 12, 25, 21, 20, 17, 2, 1}
root := createTree(values)
input1 := 12
input2 := 20
answer := findLCA(root, input1, input2)
if answer != nil {
fmt.Printf("Lowest common ancestor of %d & %d is %d\n", input1, input2, answer.Val)
} else {
fmt.Println("Could not able to find ancestor")
}
preOrderResult := []int{}
preOrderTraversal(root, &preOrderResult)
fmt.Printf("preOrderResult = %d\n", preOrderResult)
postOrderResult := []int{}
postOrderTraversal(root, &postOrderResult)
fmt.Printf("postOrderResult = %d\n", postOrderResult)
inOrderResult := []int{}
inOrderTraversal(root, &inOrderResult)
fmt.Printf("inOrderResult = %d\n", inOrderResult)
}
Output
Lowest common ancestor of 12 & 20 is 14
preOrderResult = [3 2 1 14 13 12 25 21 20 17]
postOrderResult = [1 2 12 13 17 20 21 25 14 3]
inOrderResult = [1 2 3 12 13 14 17 20 21 25] ---- sorted order
Program exited.PreOrder, PostOrder & InOrder Traversal
//The pre-order traversal is a topologically sorted one, because a parent node is processed before any of its child nodes is done.
func preOrderTraversal(root *TreeNode, result *[]int) {
if root == nil {
return
}
*result = append(*result, root.Val)
preOrderTraversal(root.Left, result)
preOrderTraversal(root.Right, result)
}
//Post-order traversal can be useful to get postfix expression of a binary expression tree.
func postOrderTraversal(root *TreeNode, result *[]int) {
if root == nil {
return
}
postOrderTraversal(root.Left, result)
postOrderTraversal(root.Right, result)
*result = append(*result, root.Val)
}
//In a binary search tree ordered such that in each node the key is greater than all keys in its left subtree and less than all keys in its right subtree, in-order traversal retrieves the keys in ascending sorted order.
func inOrderTraversal(root *TreeNode, result *[]int) {
if root == nil {
return
}
inOrderTraversal(root.Left, result)
*result = append(*result, root.Val)
inOrderTraversal(root.Right, result)
}Please visit https: https://codeandalgo.com for more such contents