UnDirected Graph Cycle Detection
Table of Contents
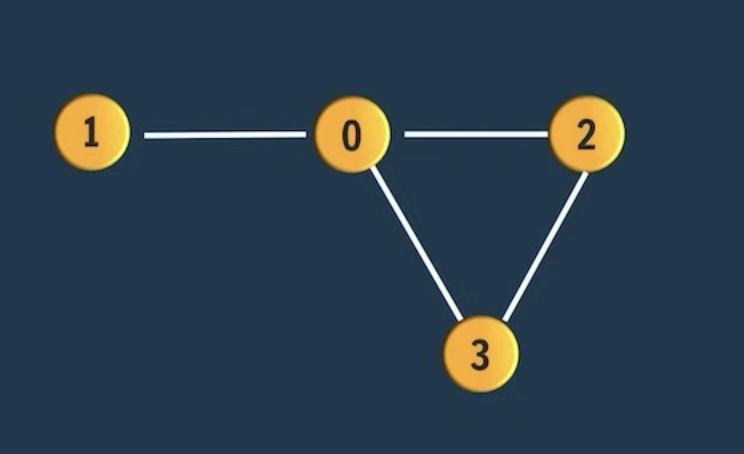
Problem Statement
Important Logic
- Here, in modified DFS, we will start returning value from DFS recursive function.
- Be careful of accepting this return value and take decision based on that.
- If neighbour is already visited and it is NOT Parent,
- then we have found cycle.
func dfs(graph map[int][]edge, visited []bool, currentVertex, parentVertex int) bool {
visited[currentVertex] = true
// visit all neighbours
for _, edge := range graph[currentVertex] {
// If neighbour is already visited and it is NOT Parent,
// then we have found cycle.
if visited[edge.destination] && edge.destination != parentVertex {
return true
}
if !visited[edge.destination] {
// Here, in modified DFS,
// we will start returning value from DFS recursive function.
// Be careful of accepting this return value
// and take decision based on that.
if dfs(graph, visited, edge.destination, currentVertex) {
return true
}
}
}
return false
}Golang Solution
package main
import (
"fmt"
)
type edge struct {
source int
destination int
}
func createEdge(graph map[int][]edge, source, destination int) {
graph[source] = append(graph[source], edge{
source: source,
destination: destination,
})
}
func createGraph() map[int][]edge {
graph := map[int][]edge{}
createEdge(graph, 0, 1)
createEdge(graph, 1, 0)
createEdge(graph, 0, 2)
createEdge(graph, 2, 0)
createEdge(graph, 0, 3)
createEdge(graph, 3, 0)
createEdge(graph, 2, 3)
createEdge(graph, 3, 2)
return graph
}
func dfs(graph map[int][]edge, visited []bool, currentVertex, parentVertex int) bool {
visited[currentVertex] = true
// visit all neighbours
for _, edge := range graph[currentVertex] {
// If neighbour is already visited and it is NOT Parent,
// then we have found cycle.
if visited[edge.destination] && edge.destination != parentVertex {
return true
}
if !visited[edge.destination] {
if dfs(graph, visited, edge.destination, currentVertex) {
return true
}
}
}
return false
}
func main() {
graph := createGraph()
maxVertex := 3
visited := make([]bool, maxVertex+1)
isCyclePresent := false
// traverse all vertices
for i := 0; i < maxVertex; i++ {
parentVertex := -1
startingVertex := i
if !visited[startingVertex] {
isCyclePresent = dfs(graph, visited, startingVertex, parentVertex)
if isCyclePresent {
fmt.Printf("Cycle exist in given graph")
break
}
}
}
if !isCyclePresent {
fmt.Printf("Cycle does NOT exist in given graph")
}
}Output
Cycle exist in given graph
Program exited.Visit https: https://codeandalgo.com for more such contents.