Graph
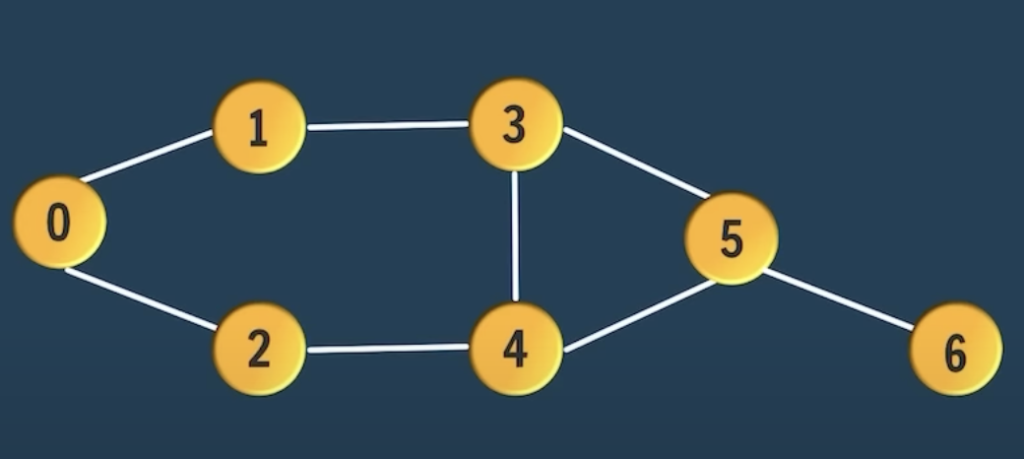
Table of Contents
Graph Representation & usage
Choosing between map[int][]edge and [][]int{} for representing graph data in Go depends on the specific requirements of your application and the characteristics of the graph you are working with. Here’s a comparison of both approaches:
Adjecancy List map[int][]edge
Advantages
- Sparsity Handling: It efficiently represents sparse graphs, where not every node has edges to every other node. Only existing edges are stored, which saves memory.
- Flexible Node Identification: Using integers as keys allows for non-continuous or arbitrary node IDs. You can easily add or remove nodes without worrying about their indices.
- Easier Edge Management: You can easily append edges to a node and dynamically manage edges without predefined structure.
Disadvantages
- Overhead: There’s a slight overhead in using maps compared to slices due to hashing and other internal mechanisms.
- Complexity: If you’re performing many operations that assume a dense representation (like matrix-based algorithms), it may require additional conversion logic.
Adjecancy Matrix[][]int{}
Advantages
- Simplicity: It can be simpler for dense graphs where the number of edges is close to the maximum possible edges (e.g., fully connected graphs).
- Direct Access: Provides O(1) access to edges if you know the indices, which can be beneficial for algorithms that frequently check for edges.
- Straightforward Representation: A 2D slice is a straightforward representation for algorithms that rely on adjacency matrices.
Disadvantages
- Space Inefficiency: It can waste space in sparse graphs because you may allocate many empty slots for non-existent edges.
- Fixed Structure: The structure is fixed; adding or removing nodes may require reshaping the matrix, which can be inefficient.
- Node ID Constraints: It’s less flexible with node IDs, requiring them to be contiguous and starting from zero, making it less versatile for dynamic graphs.
Conclusion
- Use
map[int][]edgeif you need to represent sparse graphs, have arbitrary node IDs, or require dynamic graph modifications (adding/removing nodes and edges). - Use
[][]int{}if you are working with dense graphs, need constant-time edge lookups, or are implementing algorithms that naturally fit an adjacency matrix.
In many real-world applications, especially with sparse graphs, map[int][]edge is often the preferred choice for its flexibility and efficiency. However, if your graph is dense and fits well into a fixed structure, then using [][]int{} might be simpler and more efficient.
Graph using Adjacency List
Below code covers basic graph creation.
- Create Graph
- Add Vertex and Edges in Graph
- Print all Vertices and edges corresponding to it
Golang Solution
package main
import "fmt"
type edge struct {
source int
destination int
weight int
}
func createEdge(graph map[int][]edge, source, destination, weight int) {
graph[source] = append(graph[source], edge{
source: source,
destination: destination,
weight: weight,
})
}
func createGraph(graph map[int][]edge) {
createEdge(graph, 0, 1, 0)
createEdge(graph, 0, 2, 0)
createEdge(graph, 1, 0, 0)
createEdge(graph, 1, 3, 0)
createEdge(graph, 2, 0, 0)
createEdge(graph, 2, 4, 0)
createEdge(graph, 3, 1, 0)
createEdge(graph, 3, 4, 0)
createEdge(graph, 3, 5, 0)
createEdge(graph, 4, 2, 0)
createEdge(graph, 4, 5, 0)
createEdge(graph, 4, 3, 0)
createEdge(graph, 5, 3, 0)
createEdge(graph, 5, 4, 0)
createEdge(graph, 5, 6, 0)
return
}
func printGraph(graph map[int][]edge) {
for vertex, edges := range graph {
fmt.Printf("Vertex=%d : ", vertex)
for _, edge := range edges {
fmt.Printf("%d,", edge.destination)
}
fmt.Println("")
}
}
func main() {
graph := make(map[int][]edge)
createGraph(graph)
printGraph(graph)
}
Output
Vertex=0 : 1,2,
Vertex=1 : 0,3,
Vertex=2 : 0,4,
Vertex=3 : 1,4,5,
Vertex=4 : 2,5,3,
Vertex=5 : 3,4,6,
Program exited.
BFS + Disconnected Components
BFS Important Logic
func bfs(graph map[int][]edge, visited []bool, startingVertex int) (component []int, err error) {
component = []int{}
mq := createQueue()
mq.enQueue(startingVertex)
for !mq.isEmpty() {
vertex := mq.deQueue()
if !visited[vertex] {
visited[vertex] = true
component = append(component, vertex)
for _, edge := range graph[vertex] {
if !visited[edge.destination] {
mq.enQueue(edge.destination)
}
}
}
}
return component, nil
}Full Code
package main
import (
"errors"
"fmt"
)
type edge struct {
source int
destination int
weight int
}
func createEdge(graph map[int][]edge, source, destination, weight int) {
graph[source] = append(graph[source], edge{
source: source,
destination: destination,
weight: weight,
})
}
type queue struct {
q []int
}
func (mq *queue) enQueue(item int) {
mq.q = append(mq.q, item)
}
func (mq *queue) deQueue() (item int, err error) {
if mq.isEmpty() {
return -1, errors.New("Queue is empty")
}
item = mq.q[0]
mq.q = mq.q[1:]
return item, nil
}
func (mq *queue) isEmpty() bool {
return len(mq.q) == 0
}
func createQueue() (mq *queue) {
return &queue{q: []int{}}
}
func createGraph(graph map[int][]edge) {
createEdge(graph, 0, 1, 0)
createEdge(graph, 0, 2, 0)
createEdge(graph, 1, 0, 0)
createEdge(graph, 1, 3, 0)
createEdge(graph, 2, 0, 0)
createEdge(graph, 2, 4, 0)
createEdge(graph, 3, 1, 0)
createEdge(graph, 3, 4, 0)
createEdge(graph, 3, 5, 0)
createEdge(graph, 4, 2, 0)
createEdge(graph, 4, 5, 0)
createEdge(graph, 4, 3, 0)
createEdge(graph, 5, 3, 0)
createEdge(graph, 5, 4, 0)
createEdge(graph, 5, 6, 0)
createEdge(graph, 7, 8, 0)
return
}
func printGraph(graph map[int][]edge) {
for vertex, edges := range graph {
fmt.Printf("Vertex=%d : ", vertex)
for _, edge := range edges {
fmt.Printf("%d,", edge.destination)
}
fmt.Println("")
}
}
func bfs(graph map[int][]edge, visited []bool, startingVertex int) (component []int, err error) {
// Check if graph is empty
if len(graph) == 0 {
return nil, errors.New("graph is empty")
}
// Initialize component slice and create a new queue
component = []int{}
mq := createQueue()
mq.enQueue(startingVertex)
for !mq.isEmpty() {
vertex, err := mq.deQueue()
if err != nil {
return nil, err
}
// Proceed if the vertex has not been visited
if !visited[vertex] {
visited[vertex] = true
component = append(component, vertex)
fmt.Printf("Visited vertex=%d\n", vertex)
// Enqueue unvisited neighbors
for _, edge := range graph[vertex] {
if !visited[edge.destination] {
mq.enQueue(edge.destination)
}
}
}
}
return component, nil
}
func getMaxVertex(graph map[int][]edge) int {
maxVertex := 0
for vertex := range graph {
if maxVertex < vertex {
maxVertex = vertex
}
for _, edge := range graph[vertex] {
if maxVertex < edge.destination {
maxVertex = edge.destination
}
}
}
return maxVertex
}
func main() {
graph := make(map[int][]edge)
createGraph(graph)
fmt.Println(" ---------- Graph representation using adjacency list ---------- ")
printGraph(graph)
fmt.Println(" ---------- BFS Started ---------- ")
maxVertex := getMaxVertex(graph)
visited := make([]bool, maxVertex+1)
components := [][]int{}
for vertex := range graph {
if !visited[vertex] {
component, err := bfs(graph, visited, vertex)
components = append(components, component)
if err != nil {
fmt.Println(err)
}
}
}
fmt.Println(" ---------- Disconnected Component list ---------- ")
// printing all components
for _, component := range components {
fmt.Println("Component : ", component)
}
}Output
---------- Graph representation using adjacency list ----------
Vertex=4 : 2,5,3,
Vertex=5 : 3,4,6,
Vertex=7 : 8,
Vertex=0 : 1,2,
Vertex=1 : 0,3,
Vertex=2 : 0,4,
Vertex=3 : 1,4,5,
---------- BFS Started ----------
Visited vertex=7
Visited vertex=8
Visited vertex=0
Visited vertex=1
Visited vertex=2
Visited vertex=3
Visited vertex=4
Visited vertex=5
Visited vertex=6
---------- Disconnected Component list ----------
Component : [7 8]
Component : [0 1 2 3 4 5 6]
Program exited.DFS (Depth First Search Traversal)
DFS Important Logic
func dfs(graph map[int][]edge, visited []bool, vertex int, component *[]int) {
visited[vertex] = true
*component = append(*component, vertex)
for _, edge := range graph[vertex] {
if !visited[edge.destination] {
dfs(graph, visited, edge.destination, component)
}
}
}Full Code
package main
import (
"fmt"
"sort"
)
type edge struct {
source int
destination int
}
func createEdge(graph map[int][]edge, source, destination int) {
graph[source] = append(graph[source], edge{
source: source,
destination: destination,
})
}
func createGraph() map[int][]edge {
graph := map[int][]edge{}
createEdge(graph, 0, 1)
createEdge(graph, 0, 2)
createEdge(graph, 1, 3)
createEdge(graph, 1, 0)
createEdge(graph, 2, 4)
createEdge(graph, 2, 0)
createEdge(graph, 3, 5)
createEdge(graph, 3, 4)
createEdge(graph, 3, 1)
createEdge(graph, 4, 3)
createEdge(graph, 4, 5)
createEdge(graph, 4, 2)
createEdge(graph, 5, 3)
createEdge(graph, 5, 4)
createEdge(graph, 5, 6)
createEdge(graph, 6, 5)
return graph
}
func getVertices(graph map[int][]edge) []int {
uniqueVertices := make(map[int]bool)
for vertex, edges := range graph {
uniqueVertices[vertex] = true // Add source vertex
for _, edge := range edges {
uniqueVertices[edge.destination] = true // Add destination vertex
}
}
vertices := make([]int, 0, len(uniqueVertices))
for vertex := range uniqueVertices {
vertices = append(vertices, vertex)
}
sort.Ints(vertices) // Sort vertices in ascending order
return vertices
}
func dfs(graph map[int][]edge, visited []bool, vertex int, component *[]int) {
visited[vertex] = true
*component = append(*component, vertex)
for _, edge := range graph[vertex] {
if !visited[edge.destination] {
dfs(graph, visited, edge.destination, component)
}
}
}
func main() {
graph := createGraph()
vertices := getVertices(graph)
// Determine the size of `visited` dynamically based on the maximum vertex ID
maxVertexID := vertices[len(vertices)-1]
visited := make([]bool, maxVertexID+1)
// Traverse over all vertices
for _, vertex := range vertices {
component := []int{}
if !visited[vertex] {
dfs(graph, visited, vertex, &component)
fmt.Printf("component=%#v\n", component)
}
}
}
Output
component=[]int{0, 1, 3, 5, 4, 2, 6}
Program exited.ALL PATH from Source to All Vertices DFS
Modified DFS
//All Path S to T : modified dfs
package main
import "fmt"
type edge struct {
source int
destination int
}
func createEdge(graph map[int][]edge, s, d int) {
graph[s] = append(graph[s], edge{
source: s,
destination: d,
})
}
func createGraph() map[int][]edge {
graph := map[int][]edge{}
createEdge(graph, 0, 1)
createEdge(graph, 1, 0)
createEdge(graph, 0, 2)
createEdge(graph, 2, 0)
createEdge(graph, 1, 3)
createEdge(graph, 3, 1)
createEdge(graph, 2, 4)
createEdge(graph, 4, 2)
createEdge(graph, 3, 4)
createEdge(graph, 4, 3)
createEdge(graph, 3, 5)
createEdge(graph, 5, 3)
createEdge(graph, 4, 5)
createEdge(graph, 5, 4)
createEdge(graph, 5, 6)
createEdge(graph, 6, 5)
return graph
}
func dfs(graph map[int][]edge, visited []bool, current int, path string, target int) {
// base case
if current == target {
fmt.Printf("\nPath= %#v\n", path)
return
}
visited[current] = true
for _, edge := range graph[current] {
if !visited[edge.destination] {
dfs(graph, visited, edge.destination, path+fmt.Sprintf("%d", edge.destination), target)
}
}
visited[current] = false
}
func main() {
graph := createGraph()
maxVertex := 6
source := 0
target := 5
path := fmt.Sprintf("%d", source)
visited := make([]bool, maxVertex+1)
dfs(graph, visited, source, path, target)
}Output
Path= "01345"
Path= "0135"
Path= "02435"
Path= "0245"
Program exited.Cycle Detection (DFS)
UnDirected Graph Cycle Detection
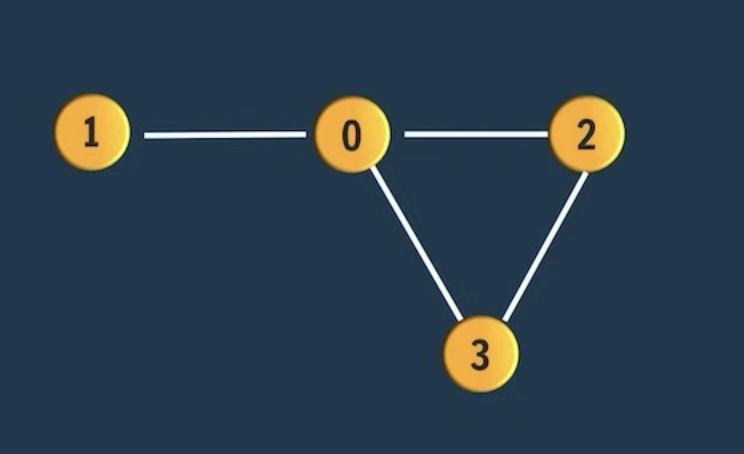
Important Logic (UnDir Graph Cycle Detection)
- Here, in modified DFS, we will start returning value from DFS recursive function.
- Be careful of accepting this return value and take decision based on that.
- If neighbour is already visited and it is NOT Parent,
- then we have found cycle.
func dfs(graph map[int][]edge, visited []bool, currentVertex, parentVertex int) bool {
visited[currentVertex] = true
// visit all neighbours
for _, edge := range graph[currentVertex] {
// If neighbour is already visited and it is NOT Parent,
// then we have found cycle.
if visited[edge.destination] && edge.destination != parentVertex {
return true
}
if !visited[edge.destination] {
// Here, in modified DFS,
// we will start returning value from DFS recursive function.
// Be careful of accepting this return value
// and take decision based on that.
if dfs(graph, visited, edge.destination, currentVertex) {
return true
}
}
}
return false
}Golang Solution
package main
import (
"fmt"
)
type edge struct {
source int
destination int
}
func createEdge(graph map[int][]edge, source, destination int) {
graph[source] = append(graph[source], edge{
source: source,
destination: destination,
})
}
func createGraph() map[int][]edge {
graph := map[int][]edge{}
createEdge(graph, 0, 1)
createEdge(graph, 1, 0)
createEdge(graph, 0, 2)
createEdge(graph, 2, 0)
createEdge(graph, 0, 3)
createEdge(graph, 3, 0)
createEdge(graph, 2, 3)
createEdge(graph, 3, 2)
return graph
}
func dfs(graph map[int][]edge, visited []bool, currentVertex, parentVertex int) bool {
visited[currentVertex] = true
// visit all neighbours
for _, edge := range graph[currentVertex] {
// If neighbour is already visited and it is NOT Parent,
// then we have found cycle.
if visited[edge.destination] && edge.destination != parentVertex {
return true
}
if !visited[edge.destination] {
if dfs(graph, visited, edge.destination, currentVertex) {
return true
}
}
}
return false
}
func main() {
graph := createGraph()
maxVertex := 3
visited := make([]bool, maxVertex+1)
isCyclePresent := false
// traverse all vertices
for i := 0; i < maxVertex; i++ {
parentVertex := -1
startingVertex := i
if !visited[startingVertex] {
isCyclePresent = dfs(graph, visited, startingVertex, parentVertex)
if isCyclePresent {
fmt.Printf("Cycle exist in given graph")
break
}
}
}
if !isCyclePresent {
fmt.Printf("Cycle does NOT exist in given graph")
}
}Output
Cycle exist in given graph
Program exited.Cycle Detection (Directed Graph) DFS
Important Logic
func dfs(graph map[int][]edge, visited []bool, current int, stack []bool) bool {
// use stack to keep track of vertex which are called in past
// if we find a vertex which is unVisited and present on stack then
// cycle is present in graph
visited[current] = true
// stack is used to check if certain vertex is present
// on current recursion stack or not
stack[current] = true
for _, edge := range graph[current] {
// if vertex is present on recursion stack
// then it mean cycle exist !
// EASY
if stack[edge.destination] {
return true
}
if !visited[edge.destination] {
if dfs(graph, visited, edge.destination, stack) {
return true
}
}
}
// important to clean up recursion STACK
// TRICKY !
stack[current] = false
return false
}Golang Solution
//practice dfs
package main
import (
"fmt"
)
type edge struct {
source int
destination int
}
func createEdge(graph map[int][]edge, s, d int) {
graph[s] = append(graph[s], edge{
source: s,
destination: d,
})
}
func createGraph() map[int][]edge {
graph := map[int][]edge{}
createEdge(graph, 0, 1)
createEdge(graph, 0, 3)
createEdge(graph, 3, 2)
// below edge creates cycle
createEdge(graph, 2, 0)
return graph
}
func dfs(graph map[int][]edge, visited []bool, current int, stack []bool) bool {
// use stack to keep track of vertex which are called in past
// if we find a vertex which is unVisited and present on stack then
// cycle is present in graph
visited[current] = true
stack[current] = true
for _, edge := range graph[current] {
// if vertex is present on recursion stack
// then it mean cycle exist !
// EASY
if stack[edge.destination] {
return true
}
if !visited[edge.destination] {
if dfs(graph, visited, edge.destination, stack) {
return true
}
}
}
// important to clean up recursion STACK
// TRICKY !
stack[current] = false
return false
}
func main() {
graph := createGraph()
maxVertex := 3
visited := make([]bool, maxVertex+1)
stack := make([]bool, maxVertex+1)
isCyclePresent := false
for i := 0; i <= maxVertex; i++ {
if !visited[i] {
isCyclePresent = dfs(graph, visited, i, stack)
if isCyclePresent {
fmt.Printf("Cycle Exist")
break
}
}
}
if !isCyclePresent {
fmt.Printf("Cycle does NOT Exist")
}
}Output
Cycle Exist
Program exited.Topological Sort (DAG) (DFS)
Directed ACyclic Graph
- Directed Acyclic graph (DAG) is a directed graph with no cycles.
- Directed Graph + NO Cycles
- Topological sort is used only for DAGs.
- It is a linear order of vertices such that such that directed edge u->v, the vertex u comes before v in the order.
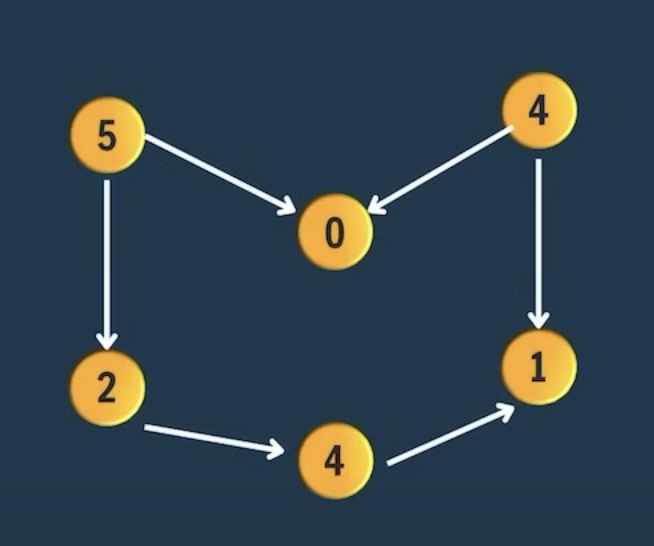
Golang Solution
//Topological Sort
//DAG - Directed Acyclic Graph
package main
import (
"fmt"
)
type edge struct {
source int
destination int
}
func createEdge(graph map[int][]edge, source, destination int) {
graph[source] = append(graph[source], edge{
source: source,
destination: destination,
})
}
func createGraph() map[int][]edge {
graph := map[int][]edge{}
createEdge(graph, 2, 3)
createEdge(graph, 3, 1)
createEdge(graph, 4, 0)
createEdge(graph, 4, 1)
createEdge(graph, 5, 0)
createEdge(graph, 5, 2)
return graph
}
func topoSortUtil(graph map[int][]edge, visited []bool, current int, stack *[]int) {
visited[current] = true
// visited neighbours
for _, edge := range graph[current] {
if !visited[edge.destination] {
topoSortUtil(graph, visited, edge.destination, stack)
}
}
// PUSH ONTO STACK
// Simple but Tricky
*stack = append(*stack, current)
}
func topoSort(graph map[int][]edge, visited []bool, maxVertex int) {
stack := []int{}
for i := 0; i <= maxVertex; i++ {
if !visited[i] {
topoSortUtil(graph, visited, i, &stack)
}
}
// print stack in REVERSE order
for j := len(stack) - 1; j >= 0; j -= 1 {
fmt.Printf("%d ", stack[j])
}
fmt.Printf("\n")
}
func main() {
graph := createGraph()
maxVertex := 5
visited := make([]bool, maxVertex+1)
topoSort(graph, visited, maxVertex)
}
Output
5 4 2 3 1 0Strongly Connected Components (SCC) DFS
SCC is component in which we can reach every vertex of the component from every other vertex in that component.
1. Kosaraju Algorithm (Topological Sort, transpose, Reverse DFS)
- Topological Sort
- Transpose Graph
- Reverse DFS
- Use DFS on Transpose Graph using vertices order given by topological sort
Kosaraju’s Algorithm Complexity
- Two DFS Passes: Kosaraju’s algorithm performs two passes of DFS, making it efficient at O(V+E) complexity, where V is the number of vertices and E is the number of edges.
- This efficiency makes Kosaraju’s algorithm particularly suitable for large graphs.
Alternative SCC Algorithms (e.g., Tarjan’s Algorithm)
- Comparison with Tarjan’s Algorithm: While Kosaraju’s algorithm uses two passes of DFS, Tarjan’s algorithm finds SCCs in a single DFS pass using low-link values and a stack.
- Kosaraju’s is simpler conceptually but requires transposing the graph, where as Tarjan’s is more intricate but avoids graph transposition.
Golang solution
package main
import (
"fmt"
)
type edge struct {
source int
destination int
}
func createEdge(graph map[int][]edge, source int, destination int) {
graph[source] = append(graph[source], edge{
source: source,
destination: destination,
})
}
func createGraph() map[int][]edge {
graph := map[int][]edge{}
createEdge(graph, 0, 2)
createEdge(graph, 2, 1)
createEdge(graph, 1, 0)
createEdge(graph, 0, 3)
createEdge(graph, 3, 4)
return graph
}
func dfs(transpose map[int][]edge, visited []bool, current int) {
visited[current] = true
fmt.Printf("%d ", current)
for _, edge := range transpose[current] {
if !visited[edge.destination] {
dfs(transpose, visited, edge.destination)
}
}
}
func topoSortUtil(graph map[int][]edge, visited []bool, current int, stack *[]int) {
visited[current] = true
for _, edge := range graph[current] {
if !visited[edge.destination] {
topoSortUtil(graph, visited, edge.destination, stack)
}
}
*stack = append(*stack, current)
}
func topoSort(graph map[int][]edge, visited []bool, vertices []int, stack *[]int) {
for _, vertex := range vertices {
if !visited[vertex] {
topoSortUtil(graph, visited, vertex, stack)
}
}
}
func kosaRajuAlgo(graph map[int][]edge, visited []bool, vertices []int) {
// 1. apply topological sort to get order of vertices in stack
stack := []int{}
topoSort(graph, visited, vertices, &stack)
// 2. Transpose graph
transpose := map[int][]edge{}
for vertex, edges := range graph {
visited[vertex] = false
for _, e := range edges {
visited[e.destination] = false
transpose[e.destination] = append(transpose[e.destination], edge{
source: e.destination,
destination: e.source,
})
}
}
// 3. Pop all item from stack and apply dfs of each vertex to get list of SCC
// in reverse order as we are using stack
for j := len(stack) - 1; j >= 0; j -= 1 {
if !visited[stack[j]] {
dfs(transpose, visited, stack[j])
fmt.Println()
}
}
}
func main() {
graph := createGraph()
vertices := []int{0, 1, 2, 3, 4}
totalVertices := len(vertices)
visited := make([]bool, totalVertices)
kosaRajuAlgo(graph, visited, vertices)
}Output
stack=[]int{1, 2, 4, 3, 0}
0 1 2
3
4
Program exited.Tarjan Algorithm (DFS)
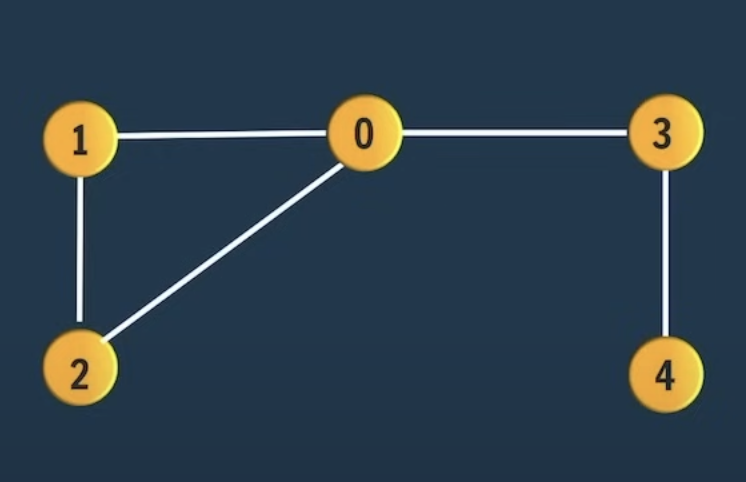
Can be used to find
- Bridge in graph
- Articulation point in graph
- Stongly connected component in graph
- Topological order
1. Bridge in graph (DFS)
- Bridge is an edge whose deletion increases the total number of connected components in a graph.
- We will need to track below metadata
- dt : discovery time
- lowest dt : lowest discovery time among neighbour nodes
Golang Solution
// Tarjan Algo- bridge edge
package main
import (
"fmt"
)
type edge struct {
source int
destination int
}
func createEdge(graph map[int][]edge, source, destination int) {
graph[source] = append(graph[source], edge{
source: source,
destination: destination,
})
}
func createGraph() map[int][]edge {
graph := map[int][]edge{}
createEdge(graph, 0, 1)
createEdge(graph, 0, 2)
createEdge(graph, 0, 3)
createEdge(graph, 1, 0)
createEdge(graph, 1, 2)
createEdge(graph, 2, 1)
createEdge(graph, 2, 0)
createEdge(graph, 3, 0)
createEdge(graph, 3, 4)
createEdge(graph, 3, 5)
createEdge(graph, 4, 3)
createEdge(graph, 4, 5)
createEdge(graph, 5, 3)
createEdge(graph, 5, 4)
return graph
}
func tarjanAlgo(graph map[int][]edge, visited []bool, dt []int, low []int, current int, parentVertex int, time int) {
time++
visited[current] = true
dt[current] = time
low[current] = dt[current]
for _, edge := range graph[current] {
// ignore parent
if edge.destination == parentVertex {
continue
}
// non visited not
// regular case
if !visited[edge.destination] {
tarjanAlgo(graph, visited, dt, low, edge.destination, current, time)
// update low
low[current] = min(low[current], low[edge.destination])
if dt[edge.source] < low[edge.destination] {
fmt.Printf("Bridge edge : %d-%d\n", edge.source, edge.destination)
}
}
if visited[edge.destination] {
// update low using dt of neighbour
// TRICKY !
low[current] = min(low[current], dt[edge.destination])
}
}
}
func min(a, b int) int {
if a > b {
return b
}
return a
}
func main() {
vertices := []int{0, 1, 2, 3, 4, 5}
totalVertices := len(vertices) + 1
parentVertex := -1
time := 0
graph := createGraph()
dt := make([]int, totalVertices)
low := make([]int, totalVertices)
visited := make([]bool, totalVertices)
for _, vertex := range vertices {
if !visited[vertex] {
tarjanAlgo(graph, visited, dt, low, vertex, parentVertex, time)
}
}
}Output
Bridge edge : 0-3
Program exited.
2. Articulation Point (DFS)
- Vertex in an undirected connected graph is an Articulation point (or cut vertex) , if removing it (and edges through it) disconnects the graph
- Ancestor : A node that was discovered before current node in DFS, it an Ancestor of current.
Golang Solution
//Articulation Point - Tarjan Algo
package main
import (
"fmt"
)
type edge struct {
source int
destination int
}
func createEdge(graph map[int][]edge, source, destination int) {
graph[source] = append(graph[source], edge{
source: source,
destination: destination,
})
}
func createGraph() map[int][]edge {
graph := map[int][]edge{}
createEdge(graph, 0, 1)
createEdge(graph, 0, 2)
createEdge(graph, 0, 3)
createEdge(graph, 1, 0)
createEdge(graph, 1, 2)
createEdge(graph, 2, 1)
createEdge(graph, 2, 0)
createEdge(graph, 3, 0)
createEdge(graph, 3, 4)
createEdge(graph, 3, 5)
createEdge(graph, 4, 3)
createEdge(graph, 4, 5)
createEdge(graph, 5, 3)
createEdge(graph, 5, 4)
return graph
}
func tarjanAlgo(graph map[int][]edge, visited []bool, dt []int, low []int, current int, parentVertex int, time int, ap *[]int) {
time++
visited[current] = true
dt[current] = time
low[current] = dt[current]
disconnectedChildren := 0
for _, edge := range graph[current] {
// ignore parentVertex
if edge.destination == parentVertex {
continue
}
// non visited not
// regular case
if !visited[edge.destination] {
tarjanAlgo(graph, visited, dt, low, edge.destination, current, time, ap)
// update low
low[current] = min(low[current], low[edge.destination])
// TRICKY
// check <= equal to condition here
// a) cycle u-> v with backedge
// dt[edge.source]==low[edge.destination]
// b) bridge u-> v
// dt[edge.source] <low[edge.destination]
if dt[edge.source] <= low[edge.destination] && parentVertex != -1 {
*ap = append(*ap, current)
//fmt.Printf("Articulation point : %d\n", current)
}
disconnectedChildren++
}
// similar to cycle condition in undirected graph
// but without parent check
if visited[edge.destination] {
// update low
// TRICKY !
low[current] = min(low[current], dt[edge.destination])
}
}
if disconnectedChildren > 1 && parentVertex == -1 {
*ap = append(*ap, current)
// fmt.Printf("Articulation point : %d\n", current)
}
}
func min(a, b int) int {
if a > b {
return b
}
return a
}
func main() {
vertices := []int{0, 1, 2, 3, 4, 5}
totalVertices := len(vertices) + 1
parentVertex := -1
time := 0
graph := createGraph()
dt := make([]int, totalVertices)
low := make([]int, totalVertices)
visited := make([]bool, totalVertices)
ap := []int{}
for _, vertex := range vertices {
if !visited[vertex] {
tarjanAlgo(graph, visited, dt, low, vertex, parentVertex, time, &ap)
}
}
fmt.Printf("Articulation Points : %#v\n", ap)
}
Output
Articulation Points : []int{3, 0}SHORTEST PATH from Source to All Vertices (BFS)
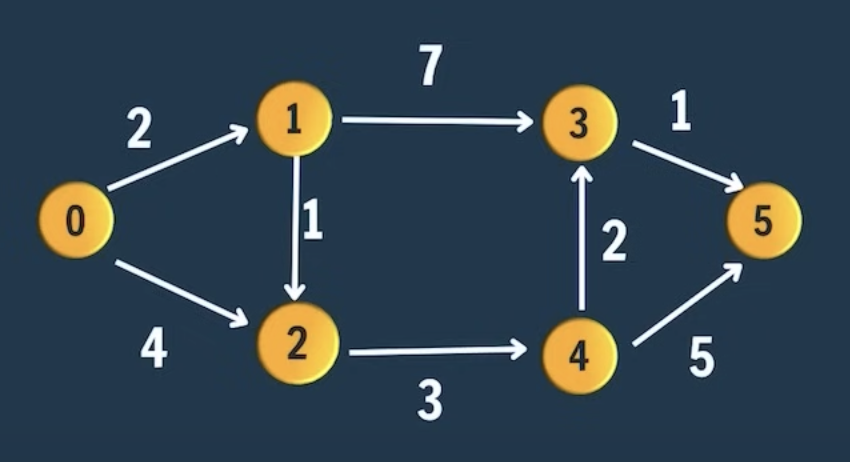
1. Dijkstra’s Algorithm (+ve edge) (BFS)
- Use priority queue with {vertex, dist[vertex]}
- Use BFS and get min distance vertex for processing
Golang solution
//Dijkstra Algo - Shortest path source to all destination
// expected Source = 0 , distance=[]int{0, 2, 3, 8, 6, 9}
// O(E + ElogV)
package main
import (
"errors"
"fmt"
"math"
"sort"
)
type pair struct {
vertex int
distance int
}
type priorityQ struct {
q []pair
}
func (pq *priorityQ) enQueue(entry pair) {
pq.q = append(pq.q, entry)
sort.Slice(pq.q, func(i, j int) bool {
return pq.q[i].distance < pq.q[j].distance
})
}
func (pq *priorityQ) deQueue() (pair, error) {
if pq.isEmpty() {
return pair{}, errors.New("Queue is empty")
}
entry := pq.q[0]
pq.q = pq.q[1:]
return entry, nil
}
func (pq *priorityQ) isEmpty() bool {
return len(pq.q) == 0
}
type edge struct {
source int
destination int
weight int
}
func createEdge(graph map[int][]edge, source, destination, weight int) {
graph[source] = append(graph[source], edge{
source: source,
destination: destination,
weight: weight,
})
}
func createGraph() map[int][]edge {
graph := map[int][]edge{}
createEdge(graph, 0, 1, 2)
createEdge(graph, 0, 2, 4)
createEdge(graph, 1, 2, 1)
createEdge(graph, 1, 3, 7)
createEdge(graph, 2, 4, 3)
createEdge(graph, 3, 5, 1)
createEdge(graph, 4, 3, 2)
createEdge(graph, 4, 5, 5)
return graph
}
func dijkstra(graph map[int][]edge, visited []bool, source int, distance []int) error {
for i := 0; i < len(distance); i++ {
if i != source {
// max signed int value
distance[i] = math.MaxInt32
//distance[i] = 1<<31 - 1
}
}
pq := &priorityQ{
q: []pair{},
}
// enqueue 1st item in queue
pq.enQueue(pair{
vertex: source,
distance: distance[source],
})
for !pq.isEmpty() {
current, err := pq.deQueue()
if err != nil {
return err
}
if !visited[current.vertex] {
visited[current.vertex] = true
// visite all neighbours
for _, edge := range graph[current.vertex] {
if !visited[edge.destination] {
if distance[edge.destination] > distance[current.vertex]+edge.weight {
distance[edge.destination] = distance[current.vertex] + edge.weight
}
pq.enQueue(pair{
vertex: edge.destination,
distance: distance[edge.destination],
})
}
}
}
}
return nil
}
func main() {
graph := createGraph()
vertices := []int{0, 1, 2, 3, 4, 5}
totalVertices := len(vertices)
visited := make([]bool, totalVertices)
distance := make([]int, totalVertices)
source := 0
err := dijkstra(graph, visited, source, distance)
if err != nil {
fmt.Printf("BFS error = %#v", err)
}
fmt.Printf("Source = %d , distance=%#v\n", source, distance)
}
Output
Source = 0 , distance=[]int{0, 2, 3, 8, 6, 9}
Program exited.2. BellmanFord Algorithm (+ve, -ve) (BFS)
- Dijkstra’s Algorithm does NOT work correctly for negative (-ve) edge weights.
- Prepare list of all edges
- Use loop from 0 to V-1
- Traverse over all edges and update distance of neighbour
- Edge case : Negative weight cycle
- Here, BellmanFord algo will FAIL
- Safety check to detect -ve weight cycle:
- Apply all edge loop one more time to check if negative weight cycle exist or not
Golang Solution
//Bellman_ford_shorted_path
package main
import (
"errors"
"fmt"
"math"
"sort"
)
type pair struct {
vertex int
dist int
}
type priorityQ struct {
q []pair
}
func (pq *priorityQ) enQueue(entry pair) {
pq.q = append(pq.q, entry)
sort.Slice(pq.q, func(i, j int) bool {
return pq.q[i].dist < pq.q[j].dist
})
}
func (pq *priorityQ) deQueue() (pair, error) {
if pq.isEmpty() {
return pair{}, errors.New("Priority Queue is empty")
}
entry := pq.q[0]
pq.q = pq.q[1:]
return entry, nil
}
func (pq *priorityQ) isEmpty() bool {
return len(pq.q) == 0
}
type edge struct {
source int
destination int
weight int
}
func createEdge(graph map[int][]edge, src, dest, wt int) {
graph[src] = append(graph[src], edge{
source: src,
destination: dest,
weight: wt,
})
}
func createGraph() map[int][]edge {
graph := map[int][]edge{}
createEdge(graph, 0, 1, 2)
createEdge(graph, 0, 2, 4)
createEdge(graph, 1, 2, -4)
createEdge(graph, 2, 3, 2)
createEdge(graph, 3, 4, 4)
// for postive weight cycle
createEdge(graph, 4, 1, -1)
// for negative weight cycle
//createEdge(graph, 4, 1, -10)
return graph
}
func bellmanFord(graph map[int][]edge, totalVertices int) []int {
distance := make([]int, totalVertices)
sourceVertex := 0
for i := 0; i < totalVertices; i++ {
distance[i] = math.MaxInt32
}
distance[sourceVertex] = 0
pq := &priorityQ{}
pq.enQueue(pair{
vertex: 0,
dist: 0,
})
for i := 0; i < totalVertices; i++ {
for _, edges := range graph {
for _, edge := range edges {
if distance[edge.source] != math.MaxInt32 && distance[edge.source]+edge.weight < distance[edge.destination] {
distance[edge.destination] = distance[edge.source] + edge.weight
}
}
}
}
// check for negative weight cycle
for _, edges := range graph {
for _, edge := range edges {
if distance[edge.source] != math.MaxInt32 && distance[edge.source]+edge.weight < distance[edge.destination] {
fmt.Println("Negative weight cycle detected")
}
}
}
return distance
}
func main() {
vertices := []int{0, 1, 2, 3, 4}
totalVertices := len(vertices)
//visited := make([]bool, totalVertices)
graph := createGraph()
distance := bellmanFord(graph, totalVertices)
fmt.Printf("%#v\n", distance)
}
Output for positive weight cycle
[]int{0, 2, -2, 0, 4}
Program exited.
Output for negative weight cycle
/ if we update below edge to introduce -ve weight cycle
// for postive weight cycle
//createEdge(graph, 4, 1, -1)
// for negative weight cycle
//createEdge(graph, 4, 1, -10)
Negative weight cycle detected
[]int{0, -30, -26, -24, -20}
Program exited.
Minimum spanning Tree (BFS)
1. Prim’s Algorithm (BFS)
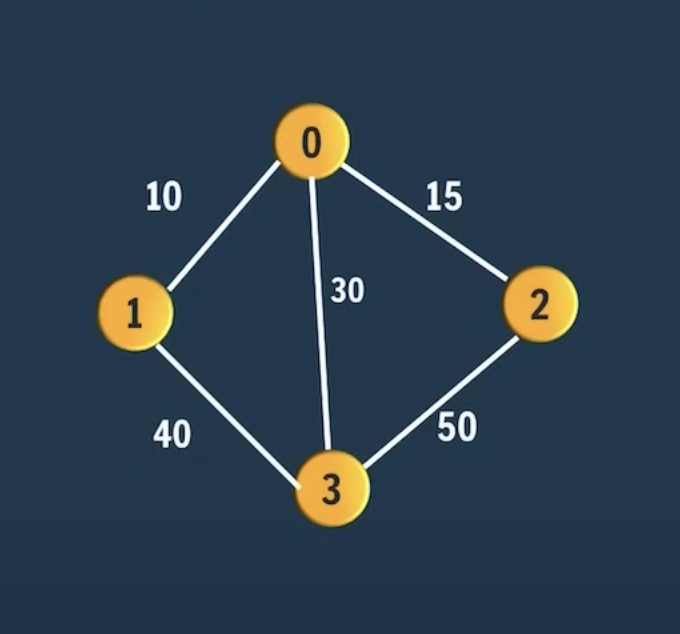
Minimum Spanning Tree
- Minimum spanning tree (MST) or minimum weight spanning tree is a
- subset of edges of a connected, edge-weighted, undirected graph
- that connects all the vertices together
- without any cycles
- & with minimum possible total graph edge weight.
Golang Solution
- Problem
- In undirected graph reverse edge was missed by creating graph.
//MST Prim's Algo
// Problem
// in undirected graph reverse edge was missed by creating graph.
// connected
// weighted
// no cycles
// undirected
// MST Set
// Non MST Set
// BFS
// as soon as we move nonMST(PQ) to MST (visited)
// add dequeued item into MST
// and update total edge weight
// a) we can also save edges at this point
// but for that we need to push edge s, d vertex in PQ
package main
import (
"errors"
"fmt"
"sort"
)
type edge struct {
source int
destination int
weight int
}
func createEdge(graph map[int][]edge, s, d, wt int) {
graph[s] = append(graph[s], edge{
source: s,
destination: d,
weight: wt,
})
}
func createGraph() map[int][]edge {
graph := map[int][]edge{}
createEdge(graph, 0, 1, 10)
createEdge(graph, 0, 2, 15)
createEdge(graph, 0, 3, 20)
createEdge(graph, 1, 0, 10)
createEdge(graph, 1, 3, 3)
createEdge(graph, 2, 0, 15)
createEdge(graph, 2, 3, 4)
createEdge(graph, 3, 0, 20)
createEdge(graph, 3, 1, 3)
createEdge(graph, 3, 2, 4)
return graph
}
type priorityQ struct {
q []edge
}
func createPriorityQ() *priorityQ {
return &priorityQ{
q: []edge{},
}
}
func (pq *priorityQ) enQueue(e edge) {
pq.q = append(pq.q, e)
sort.Slice(pq.q, func(i, j int) bool {
return pq.q[i].weight < pq.q[j].weight
})
}
func (pq *priorityQ) deQueue() (edge, error) {
if pq.isEmpty() {
return edge{}, errors.New("PriorityQueue is empty")
}
item := pq.q[0]
pq.q = pq.q[1:]
return item, nil
}
func (pq *priorityQ) isEmpty() bool {
return len(pq.q) == 0
}
func mstAlgo(graph map[int][]edge, visited []bool, startingVertex int) ([]edge, int) {
totalWt := 0
mst := []edge{}
pq := createPriorityQ()
pq.enQueue(edge{
source: startingVertex,
destination: startingVertex,
weight: 0,
})
for !pq.isEmpty() {
item, err := pq.deQueue()
if err != nil {
fmt.Printf("deQueue err = %#v\n", err)
return []edge{}, -1
}
if !visited[item.destination] {
if item.source != item.destination {
totalWt += item.weight
mst = append(mst, edge{
source: item.source,
destination: item.destination,
weight: item.weight,
})
}
visited[item.destination] = true
for _, e := range graph[item.destination] {
if !visited[e.destination] {
pq.enQueue(edge{
source: e.source,
destination: e.destination,
weight: e.weight,
})
}
}
}
}
return mst, totalWt
}
func main() {
graph := createGraph()
vertices := []int{0, 1, 2, 3}
totalVertices := len(vertices)
visited := make([]bool, totalVertices)
startingVertex := 0
mst, totalWt := mstAlgo(graph, visited, startingVertex)
fmt.Printf("Total mst graph weight=%d\n", totalWt)
for _, edge := range mst {
fmt.Printf("MST edge= %#v\n", edge)
}
}
Output
Total mst graph weight=17
MST edge= main.edge{source:0, destination:1, weight:10}
MST edge= main.edge{source:1, destination:3, weight:3}
MST edge= main.edge{source:3, destination:2, weight:4}
// Input Graph-2
// createEdge(graph, 0, 1, 10)
// createEdge(graph, 0, 2, 15)
// createEdge(graph, 0, 3, 30)
// createEdge(graph, 1, 0, 10)
// createEdge(graph, 1, 3, 40)
// createEdge(graph, 2, 0, 15)
// createEdge(graph, 2, 3, 50)
// createEdge(graph, 3, 0, 30)
// createEdge(graph, 3, 1, 40)
// createEdge(graph, 3, 2, 50)
// Output MST-2
Total mst graph weight=55
MST edge= main.edge{source:0, destination:1, weight:10}
MST edge= main.edge{source:0, destination:2, weight:15}
MST edge= main.edge{source:0, destination:3, weight:30}
Graph Interview Questions for practice
Rotting Oranges (M)
Number of Island (M)
Escape the Spreading Fire (H)
Course Schedule (M)
Find Eventual Safe States (M)
Quick Revision
BFS Important Logic
func bfs(graph map[int][]edge, visited []bool, startingVertex int) (component []int, err error) {
component = []int{}
mq := createQueue()
mq.enQueue(startingVertex)
for !mq.isEmpty() {
vertex := mq.deQueue()
if !visited[vertex] {
visited[vertex] = true
component = append(component, vertex)
for _, edge := range graph[vertex] {
if !visited[edge.destination] {
mq.enQueue(edge.destination)
}
}
}
}
return component, nil
}DFS Important Logic
func dfs(graph map[int][]edge, visited []bool, vertex int, component *[]int) {
visited[vertex] = true
*component = append(*component, vertex)
for _, edge := range graph[vertex] {
if !visited[edge.destination] {
dfs(graph, visited, edge.destination, component)
}
}
}Modified DFS Important Logic All Paths
func dfs(graph map[int][]edge, visited []bool, current int, path string, target int) {
if current == target {
fmt.Printf("\nPath= %#v\n", path)
return
}
visited[current] = true
for _, edge := range graph[current] {
if !visited[edge.destination] {
dfs(graph, visited, edge.destination, path+fmt.Sprintf("%d", edge.destination), target)
}
}
// This is extra logic added for modified DFS
// tricky !
visited[current] = false
}UnDirected Graph – Cycle Detection
func dfs(graph map[int][]edge, visited []bool, currentVertex, parentVertex int) bool {
visited[currentVertex] = true
// visit all neighbours
for _, edge := range graph[currentVertex] {
// If neighbour is already visited and it is NOT Parent,
// then we have found cycle.
if visited[edge.destination] && edge.destination != parentVertex {
return true
}
if !visited[edge.destination] {
// Here, in modified DFS,
// we will start returning value from DFS recursive function.
// Be careful of accepting this return value
// and take decision based on that.
if dfs(graph, visited, edge.destination, currentVertex) {
return true
}
}
}
return false
}Directed Graph – Cycle Detection
func dfs(graph map[int][]edge, visited []bool, current int, stack []bool) bool {
// use stack to keep track of vertex which are called in past
// if we find a vertex which is unVisited and present on stack then
// cycle is present in graph
visited[current] = true
stack[current] = true
for _, edge := range graph[current] {
// if vertex is present on recursion stack
// then it mean cycle exist !
// EASY
if stack[edge.destination] {
return true
}
if !visited[edge.destination] {
if dfs(graph, visited, edge.destination, stack) {
return true
}
}
}
// important to clean up recursion STACK
// TRICKY !
stack[current] = false
return false
}Directed Graph + No Cycle Topological Sort
func topoSortUtil(graph map[int][]edge, visited []bool, current int, stack *[]int) {
visited[current] = true
// visited neighbours
for _, edge := range graph[current] {
if !visited[edge.destination] {
topoSortUtil(graph, visited, edge.destination, stack)
}
}
// PUSH ONTO STACK
// Simple but Tricky
*stack = append(*stack, current)
}KosaRaju Algo – SCC
func kosaRajuAlgo(graph map[int][]edge, visited []bool, vertices []int) {
// 1. apply topological sort to get order of vertices in stack
stack := []int{}
topoSort(graph, visited, vertices, &stack)
// 2. Transpose graph
transpose := map[int][]edge{}
for vertex, edges := range graph {
visited[vertex] = false
for _, e := range edges {
visited[e.destination] = false
transpose[e.destination] = append(transpose[e.destination], edge{
source: e.destination,
destination: e.source,
})
}
}
// 3. Pop all item from stack and apply dfs of each vertex to get list of SCC
// in reverse order as we are using stack
for j := len(stack) - 1; j >= 0; j -= 1 {
if !visited[stack[j]] {
dfs(transpose, visited, stack[j])
fmt.Println()
}
}
}Tarjan Algorithm – Bridge
- dt : discovery time
- low: lowest discovery among neighbours
func tarjanAlgo(graph map[int][]edge, visited []bool, dt []int, low []int, current int, parentVertex int, time int) {
time++
visited[current] = true
dt[current] = time
low[current] = dt[current]
for _, edge := range graph[current] {
// ignore parent
if edge.destination == parentVertex {
continue
}
// non visited not
// regular case
if !visited[edge.destination] {
tarjanAlgo(graph, visited, dt, low, edge.destination, current, time)
// update low
low[current] = min(low[current], low[edge.destination])
if dt[edge.source] < low[edge.destination] {
fmt.Printf("Bridge edge : %d-%d\n", edge.source, edge.destination)
}
}
if visited[edge.destination] {
// update low using dt of neighbour
// TRICKY !
low[current] = min(low[current], dt[edge.destination])
}
}
}Tarjan Algorithm – Articulation Point
- dt : discovery time
- low: lowest discovery among neighbours
- ancestor : vertex visited earlier before reaching to current vertex
- #children
func tarjanAlgo(graph map[int][]edge, visited []bool, dt []int, low []int, current int, parentVertex int, time int) {
time++
visited[current] = true
dt[current] = time
low[current] = dt[current]
children := 0
for _, edge := range graph[current] {
// ignore parent
if edge.destination == parentVertex {
continue
}
// non visited not
// regular case
if !visited[edge.destination] {
children++
tarjanAlgo(graph, visited, dt, low, edge.destination, current, time)
// update low
low[current] = min(low[current], low[edge.destination])
// TRICKY
// 1. check <= equal to condition here
// a) cycle u-> v with backedge
// dt[edge.source]==low[edge.destination]
// b) bridge u-> v
// dt[edge.source] <low[edge.destination]
if dt[edge.source] <= low[edge.destination] && parent != -1 {
fmt.Printf("AP : %d\n", current)
}
}
if visited[edge.destination] {
// update low using dt of neighbour
// TRICKY !
low[current] = min(low[current], dt[edge.destination])
}
if children > 1 && parent == -1 {
fmt.Printf("AP : %d\n", current)
// articulation point found i.e. current
}
}
}Visit https: https://codeandalgo.com for more such contents